Tarea 5…………

¿Cuáles son los parámetros que forman la estructura de una onda?. Utiliza  diversos recursos para realizar la graficación de la misma.

Los parámetros de una onda son la amplitud, longitud de onda, período, frecuencia, velocidad de la onda, y la ecuación de onda.

En una onda podemos observar;

La amplitud, se lo denomina a la altura máxima que alcanza cada punto del medio al ser perturbado, es decir, la altura máxima de la perturbación.

La longitud de onda, es la distancia que se recorre por la perturbación al realizar una onda completa. ( )

El período es el tiempo asociado a la longitud de onda que tarda para realizarse una onda toda completa. ( )

La frecuencia es la cantidad de oscilaciones completas que se realizan en la unidad del tiempo, existe entre la frecuencia y el período una relación matemática , una es la inversa del otro.

La velocidad de onda, depende del tipo de la onda y del medio en el que se propaga; como la velocidad es la distancia recorrida dividiendo el tiempo que tarda en recorrer dicha distancia ( ) si en lugar de tener una distancia cualquiera tenemos una longitud de onda ( ) el tiempo empleado será el período (T) por lo tanto la velocidad de propagación de la onda se podrá calcular. V=

La ecuación de la onda, es una onda que se propaga a partir del sistema que emite y a medida que se analiza, provoca oscilaciones de algún tipo en los puntos del espacio de alcance. Es posible descubrir este proceso con una canción que permita predecir el estado de cualquier punto alcanzado por la onda en cualquier instante del tiempo.

 Mas definiciones y algunos ejemplos que son referentes a esto mismo:

Periodo (T): es el tiempo que tarda en producirse un ciclo completo de la onda sonora. Su unidad es elsegundo.

     Frecuencia (f): es el número de ciclos que se realizan por segundo. Por tanto es la inversa del periodo. Se mide en Hz.

Nota musical	f (Hz)	l (m)
DO de un tubo de órgano de 9,60 m (mínima frecuencia audible)	16	21,5
LA (contraoctava, última nota del piano)	27	12,7
DO (contraoctava)	32	10,7
DO (gran octava)	64	5,4
DO (pequeña octava)	128	2,7
DO (octava central)	256	1,35
DO (primera octava)	512	0,67
FA (tercera octava: máximo para la sensibilidad auditiva)	2.734	0,125
DO (cuarta octava, límite derecho del piano)	4.096	0,85
Máxima frecuencia audible	20.000	0,017

Tabla. Frecuencia de algunas notas y longitudes de onda correspondientes, en el aire a 20º C (c = 344 m/s)

     Velocidad del sonido (c): es la velocidad a la que se propaga la onda acústica en un medio elástico, y sólo dependerá de las características de éste. Se representa por c y se mide en m/s.

     A continuación se muestran dos tablas con algunos ejemplos de velocidades de propagación de la onda acústica, en diferentes medios y a unas condiciones determinadas:

  

Sólidos y líquidos en condiciones normales de P y Tª

sustancia	densidad (Kg/m3)	velocidad "c" (m/s)
Aluminio	2700	5104
Cobre	8900	3560
Hierro	7800	5000
Plomo	11400	1227
Mármol	2700	3810
Agua	998	1473
Agua de mar	1020	1460
Alcohol etílico	790	1220
Gasolina	700	1166

Gas en condiciones normales de P y Tª

sustancia	densidad (Kg/m3)	velocidad "c" (m/s)
Hidrógeno	90	1262
Vapor de agua	808	401
Aire	1293	344
Oxígeno	1430	317,2
Anhídrido carbónico	1970	258
Cloro	3220	206,4

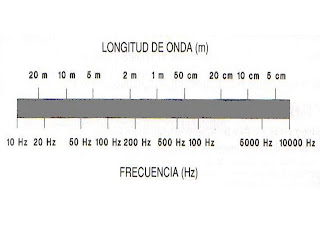
     Longitud de onda (l): es la distancia entre puntos análogos en dos ondas sucesivas. Se mide en metros.

     La longitud de onda está relacionada con la velocidad del sonido, frecuencia y periodo, por la expresión:

    

     Para sonidos propagándose en aire, dentro del rango de frecuencias audibles, los límites de la longitud de onda son de 17m para 20 Hz y 17 mm para 20000 Hz.

.Movimiento armónico simple

Se abrevia m.a,s

A este también se le puede llamar movimiento periódico y queda descreto en una función ya sea seno o coseno.

En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.Evolución en el tiempo del desplazamiento, la velocidad y la aceleración en un movimiento armónico simple.

El movimiento armónico simple es un movimiento periódico de vaivén, en el que un cuerpo oscila a un lado y a otro de su posición de equilibrio, en una dirección determinada, y en intervalos iguales de tiempo.

Algún ejemplo:

es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo. El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja. Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.

Movimiento vibratorio

Movimiento vibratorio: Es un movimiento oscilatorio que tiene su origen en el punto medio, de forma que las separaciones a ambos lados, llamadas amplitudes, son iguales.

Movimiento vibratorio armónico simple: es un movimiento vibratorio con aceleración variable, producido por una fuerza que se origina cuando el cuerpo se separa de su posición de equilibrio.

Algún ejemplo lo es:

Un resorte cuando lo separamos de su posición de equilibrio, estirándolo o comprimiéndolo, adquiere un movimiento vibratorio armónico simple, pues la fuerza recuperadora de ese resorte es la que genera una aceleración, la cual le confiere ese movimiento de vaivén.

La ecuación para poder calcular el movimiento vibratorio:

donde veremos la relación entre las magnitudes que intervienen e influyen sobre él. Como cualquier movimiento, debemos encontrar una ecuación que nos relacione la posición (x) con el tiempo, es decir, encontrar la expresión de la posición en función del tiempo. Para ello vamos a partir de dos leyes muy conocidas en Física:

- Ley de Hooke: que determina que la fuerza recuperadora del resorte es proporcional a la posición y de signo contrario. La expresión de la ley es:

F = - Kx

- La 2ª ley de Newton: que nos viene a decir que toda aceleración tiene su origen en una fuerza. Esto lo expresamos con la conocida:

F = ma

Es obvio que la fuerza recuperadora del resorte es la que origina la aceleración del movimiento, lo que supone que ambas fuerzas, expresadas arriba, son iguales. Luego:

Donde hemos expresado la aceleración como la segunda derivada de la posición con respecto al tiempo. A partir de esta ecuación encontramos dos soluciones para el valor de la posición en función del tiempo:

x = A sen(wt + q) y x = A cos(wt + q)

siendo x la elongación, A la amplitud, w la pulsación o frecuencia angular y q el desfase, que nos indica la discrepancia entre el origen de espacios (pinto donde empezamos a medir el espacio) y el origen de tiempos.

Movimiento ondulatorio

El movimiento ondulatorio se mide por la frecuencia, es decir, por el número de ciclos u oscilaciones que tiene por segundo.

La unidad de frecuencia es el hertz (Hz), que equivale a un ciclo por segundo.

El sonido es un tipo de onda que se propaga únicamente en presencia de un medio que haga de soporte de la perturbación.

 El movimiento ondulatorio supone únicamente un transporte de energía y de cantidad de movimiento.

Junto a una primera clasificación de las ondas en mecánicas y electromagnéticas, es posible distinguir diferentes tipos de ondas atendiendo a criterios distintos. En relación con su ámbito de propagación las ondas pueden clasificarse en:

Monodimensionales: Son aquellas que, como las ondas en los muelles o en las cuerdas, se propagan a lo largo de una sola dirección del espacio.

Bidimensionales: Se propagan en cualquiera de las direcciones de un plano de una superficie. Se denominan también ondas superficiales y a este grupo pertenecen las ondas que se producen en la superficie de un lago cuando se deja caer una piedra sobre él. Atendiendo a la periodicidad de la perturbación local que las origina, las ondas se clasifican en:

Periódicas: Corresponden a la propagación de perturbaciones de características periódicas, como vibraciones u oscilaciones que suponen variaciones repetitivas de alguna propiedad. Así, en una cuerda unida por uno de sus extremos a un vibrador se propagará una onda periódica.

No periódicas: La perturbación que las origina se da aisladamente y en el caso de que se repita, las perturbaciones sucesivas tienen características diferentes. Las ondas aisladas, como en el caso de las fichas de dominó, se denominan también pulsos. Según que la dirección de propagación coincida o no con la dirección en la que se produce la perturbación, las ondas pueden ser:

Longitudinales: El movimiento local del medio alcanzado por la perturbación se efectúa en la dirección de avance de la onda. Un muelle que se comprime da lugar a una onda longitudinal.

Transversales: La perturbación del medio se lleva a cabo en dirección perpendicular a la de propagación. En las ondas producidas en la superficie del agua las partículas vibran de arriba a abajo y viceversa, mientras que el movimiento ondulatorio progresa en el plano perpendicular. Lo mismo sucede en el caso de una cuerda; cada punto vibra en vertical, pero la perturbación avanza según la dirección de la línea horizontal. Ambas son ondas transversales.

Efecto dopler:

El efecto, establece el cambio de frecuencia de un sonido de acuerdo al movimiento relativo entre la fuente del sonido y el observador. Este movimiento puede ser de la fuente, del observador o de los dos. Diríamos que el efecto Doppler asume la frecuencia de la fuente como una constante pero lo escuchado depende de las velocidades de la fuente y del observador.

Este efecto lo podemos observar en ondas de todo tipo (ondas sonoras, ondas electromagnéticas, etc.).

Ejemplos de efecto doppler

si uno está cerca de la vía del ferrocarril y escucha el silbato del tren al aproximarse, se advierte que el tono del silbido es más alto que el normal que se escucha cuando el tren está detenido. A medida que el tren se aleja, se observa que el tono que se escucha es más bajo que el normal.

En forma similar, en las pistas de carreras, el sonido de los automóviles que se acercan a la gradería es considerablemente más alto en tono que el sonido de los autos que se alejan de la gradería.

Si la fuente de sonido está fija, un oyente que se mueva hacia la fuente observará un aumento similar en el tono. Un oyente que se aleja de la fuente de sonido escuchará un sonido de menor tono.

Todos hemos notado que la altura (característica de un sonido) de la sirena de una ambulancia que se aproxima se reduce bruscamente cuando la ambulancia pasa al lado nuestro para alejarse.

Cuando la ambulancia se acerca, las ondas provenientes de la sirena se comprimen, es decir, el tamaño de las ondas disminuye, lo cual se traduce en la percepción de una frecuencia o altura mayor. Cuando la ambulancia se aleja, las ondas se separan en relación con el observador causando que la frecuencia observada sea menor que la de la fuente.  

Consideremos el caso de las ondas en la superficie del agua: supongamos que en el centro de un estanque hay un bicho moviendo sus patas periódicamente. Si las ondas se originan en un punto, se moverán desde ese punto en todas direcciones. Como cada perturbación viaja por el mismo medio, todas las ondas viajarán a la misma velocidad y el patrón producido por el movimiento del bicho sería un conjunto de círculos concéntricos. Estos círculos alcanzarán los bordes del estanque a la misma velocidad. Un observador en el punto A (a la izquierda) observaría la llegada de las perturbaciones con la misma frecuencia que otro B (a la derecha). De hecho, la frecuencia a la cual las perturbaciones llegarían al borde sería la misma que la frecuencia a la cual el bicho las produce. Si el bicho produjera 2 perturbaciones por segundo, entonces cada observador

 detectaría 2 perturbaciones por segundo.

Es importante notar que el efecto no se debe a un cambio real de la frecuencia de la fuente. En el ejemplo anterior, el bicho produce en los dos casos 2 perturbaciones por segundo; sólo aparentemente para el observador al cual el bicho se acerca parece mayor. El efecto se debe a que la distancia entre B y el bicho se reduce y la distancia a A aumenta.